本記事では、強化学習の基本的な説明をし、強化学習の代表的なアルゴリズムの一つであるQ学習について、簡単なゲームを通して理解することを目標にします。
強化学習とは
強化学習は、AIが試行錯誤を通して、報酬を最大化する行動を学習する機械学習の一種です。
教師あり学習や教師なし学習とは異なり、正解データやラベルがなくても、環境との相互作用から自律的に学習することができます。
強化学習の基本要素
強化学習には、以下の3つの要素が重要です。
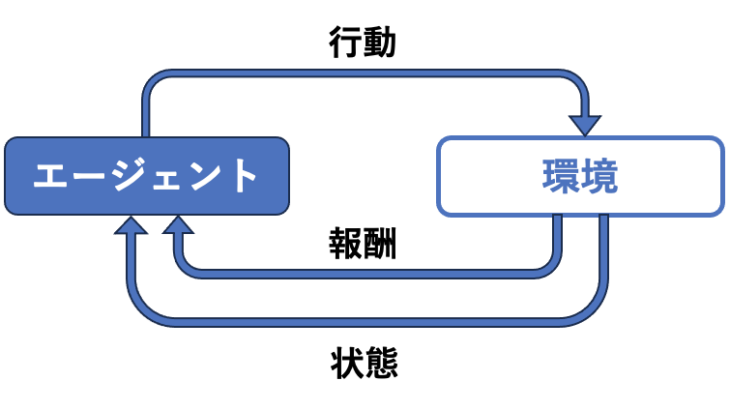
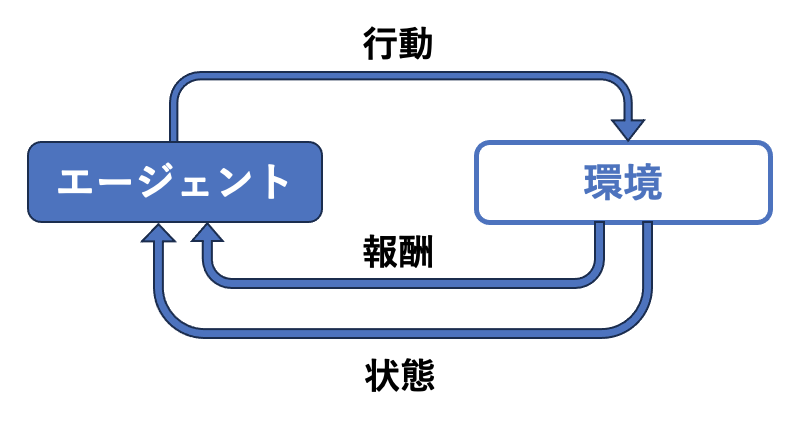
- エージェント: 学習を行うAI
- 環境: エージェントが行動する世界
- 報酬: エージェントが行動した結果得られる評価
エージェントは、環境を観察し、行動を選択し、その結果として報酬を受け取ります。エージェントは、より多くの報酬を獲得するために、状態、行動と報酬の関係(方策)を学習していきます。
強化学習のアルゴリズム
強化学習には、様々なアルゴリズムがあります。代表的なアルゴリズムは以下の通りです。
- Q学習: 状態と行動の価値関数を学習するアルゴリズム
- SARSA: 状態、行動、報酬、次の状態の4つの要素に基づいて学習するアルゴリズム
- Deep Q-Learning: 深層学習を用いてQ関数を学習するアルゴリズム
本記事では、Q学習を取り扱います。
強化学習の応用例
強化学習は、様々な分野で応用されています。以下では、いくつかの代表的な応用例を紹介します。
ゲーム
強化学習は、ゲームAIの開発において非常に有効な手法です。AlphaGoやAlphaZeroなどのプログラムは、強化学習を用いて、人間を超える棋力を獲得しました。
具体例:
- AlphaGo: 囲碁
- AlphaZero: 囲碁、将棋、チェス
- Dota 2: 5人1チームのオンラインゲーム
ロボット
強化学習は、ロボットの制御にも応用されています。ロボットは、強化学習を用いることで、環境を認識し、自律的に行動することを学習することができます。
具体例:
- 二足歩行ロボット: 歩行、階段昇降
- 倉庫ロボット: 商品のピッキングと搬送
- ドローン: 自律飛行
金融
強化学習は、金融市場での取引にも応用されています。強化学習を用いたアルゴリズムは、過去のデータに基づいて、最適な取引戦略を学習することができます。
具体例:
- 高頻度取引: 短時間で大量の取引を行う
- ポートフォリオ最適化: 資産配分を最適化する
- リスク管理: リスクを最小限に抑える
医療
強化学習は、医療分野にも応用され始めています。強化学習を用いたシステムは、患者の状態に基づいて、最適な治療計画を提案することができます。
具体例:
- 治療計画の最適化: 患者の状態に合わせて最適な治療法を選択する
- 診断支援: 医師の診断を補助する
- 薬剤開発: 新しい薬剤の開発
その他
上記以外にも、強化学習は様々な分野で応用されています。
- 製造業: 生産ラインの最適化
- エネルギー: 電力網の制御
- 教育: 個別学習の支援
- エンターテイメント: 音楽や映像の生成
Q学習
Q学習は、現在の状態である行動をとった時に、将来得られる報酬の期待値(Q値)が最大になるように学習していくアルゴリズムです。
状態\(s\)、行動\(a\)からQ値を求める関数を行動価値関数\(Q(s, a)\)といいます。
エージェントは、環境を観察して現在の状態を把握し、行動価値関数に基づいて行動を選択します。行動の結果、報酬と新しい状態を得ます。エージェントは、これらの情報を行動価値関数の更新に利用し、より良い行動を選択できるように学習していきます。
Q学習の仕組み
Q学習の仕組みは以下の3つのステップで説明できます。
- 状態の観測: エージェントは環境を観察し、現在の状態を把握します。
- 行動の選択: エージェントは行動価値関数に基づいてQ値が最大となる行動を選択します。通常、ε-グリーディ法と呼ばれる手法を用いて、一定の確率で行動価値関数を使わずにランダムな行動を選択します。
- 報酬の獲得と行動価値関数の更新: 行動の結果、報酬と新しい状態を得ます。エージェントは、これらの情報と現在の行動価値関数を用いて、次の式で行動価値関数を更新します。
$$
Q(s,a) \longleftarrow (1-\alpha)Q(s,a) + \alpha (r' + \gamma \max_{a} Q(s', a))
$$
- \(s\): 現在の状態
- \(s'\): 次の状態
- \(a\): 選択した行動
- \(r'\): 獲得した報酬
- \(\gamma\): 割引率(\(0<\gamma<1\)。未来の報酬をどれくらい重要視するかを示す値。0に近いほど直近の未来の報酬を重要視し、1に近いほど遠い未来の報酬も重要視する。)
- \(\max_{a} Q(s', a)\): 次の状態における行動価値関数の最大値
- \(\alpha\): 学習率
ε-グリーディ法
通常、行動選択の際にはQ値の大きい行動を優先しますが、
初期のランダムに決まったQ値がたまたま大きな値となった行動だけが常に選択されてしまいます。そこで、ある適当な定数ε(\(0<ε<1\))を用意して、行動選択の際に0〜1の間の乱数を生成し、
- その値がε以下: ランダムに行動を選択する
- εより大きい: Q値の大きい行動を選択する
こうすることで、Q値の初期値に依存することなく、様々な行動に対する適切なQ値の学習が可能となります。
ジャンケンゲーム
エージェントが環境にいる相手とジャンケンをする状況を考え、強化学習でジャンケンを扱えるようにします。
時刻\(t\)において、
- 環境の状態 : \(s_t\): 前回相手が出した手(今回相手が出す手は、次の時刻の環境の状態 \(s_{t+1}\) となることに注意)
- エージェントの行動\(a_t\): 今回エージェントが出す手
- 報酬\(r_t\): エージェントが勝った場合は\(1\)、相手が勝った場合は\(-1\)、あいこの場合は\(0\)の報酬を受け取る
と考えます。
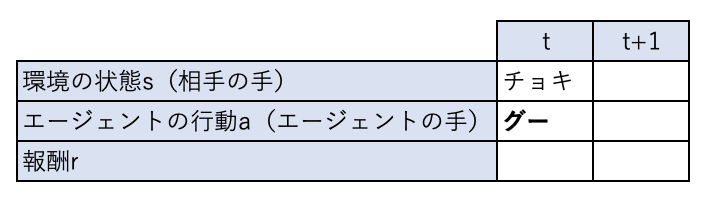
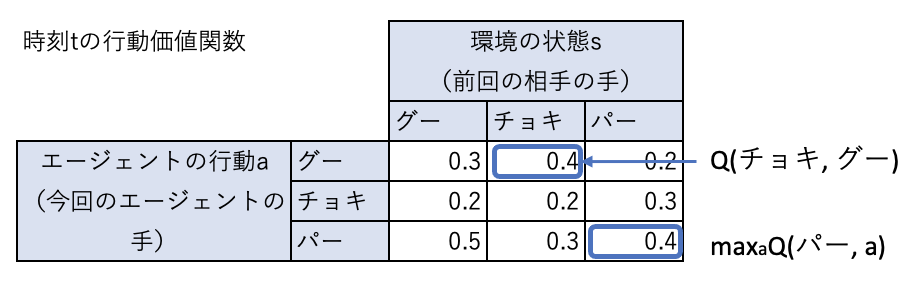
時刻\(t\)の行動価値関数が下表のようになっているとします。
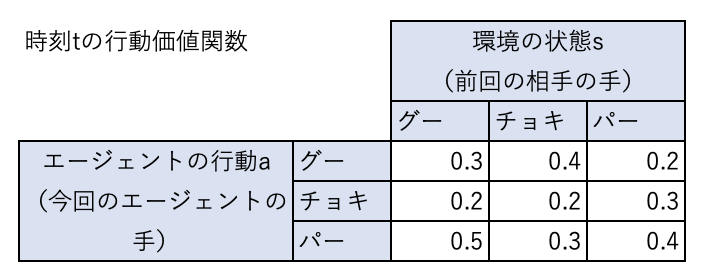
前回相手の出した手がチョキだとすると、エージェントは行動価値関数が最大になる行動をするため、グーを出すことになります。
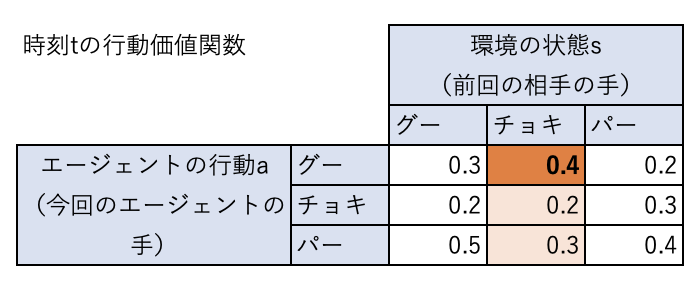
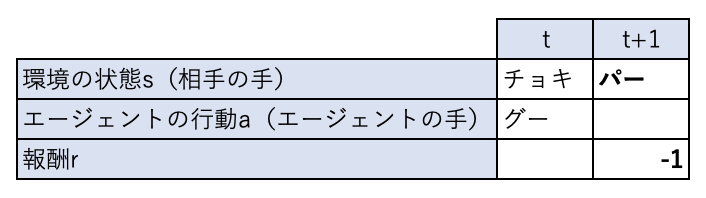
エージェントが行動すると、時刻は進んで\(t+1\)になります。
この時、相手がパーを出した場合(\(s_{t+1}=\)パー)、相手の勝ちなので報酬 \(r_{t+1}\)は-1となります。
この結果を元にエージェントは学習(行動価値関数の更新)を行います。
前回相手の出した手\(s_t\)はチョキ、今回エージェントの出した手\(a_t\)はグー、今回相手の出した手 \(s_{t+1}\)はパー、今回の報酬\(r_{t+1}\)は\(-1\)なので、更新則にしたがって行動価値関数は次のように更新されます(学習率\(\alpha=0.2\)、報酬の割引率\(\gamma=0.99\)とする)。
$$
Q(チョキ,グー) \leftarrow (1-0.2) Q(チョキ,グー) + 0.2 (-1 + 0.99 \max_{a} Q(パー,a))
$$
右辺の\(Q(チョキ、グー)\)は現在の行動価値関数から0.4、
\(\max_a Q(パー,a)\)は、現在の行動価値関数で、状態がバーの中で最大の値なので、0.4となります。
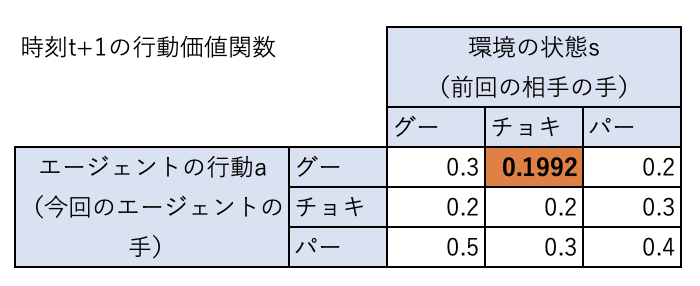
したがって、\(Q(チョキ、グー) = 0.8 \times 0.4 + 0.2 (-1 + 0.99 \times 0.4) = 0.1992\)となります。
今回の状態(チョキ)、行動(グー)の組み合わせでは負けたので、この状態、行動に対する価値が0.4から0.1992に下がっています。
ジャンケンゲームのプログラム
1ゲームで最大100回のジャンケンを行い、先にどちらかが10勝した時点でそのゲームは終了とします。
このゲームを繰り返すことで、エージェントの学習を行います。
相手の出す手がランダムだと学習のしようがないため、相手はグー→チョキ→パーを繰り返すこととします(当然エージェントはこのことを知りません)。
上記の条件のもとでQ学習のプログラムを作ります。
アルゴリズムは以下のようになります。
- 前回の相手の手 \(s_t\) と、行動価値関数\(Q(s, a)\)を元に、エージェントの出す手\(a_t\)を決定する。ただしε-グリーディ法にしたがって一定の割合でランダムな手を出す。(
Agentのget_actionメソッド) - 相手が手\(s_{t+1}\)を出し、結果を元に報酬\(r_{t+1}\)を受け取る。(
Environmentのdo_jankenメソッド) - 行動価値関数\(Q(s,a)\)を更新する。(
Agentのupdate_q_table) - どちらかが10勝するか、ジャンケンの回数が100回に達するまで1〜3を繰り返す。
なお、500ゲーム連続でエージェントの勝率が10割(最初から10連勝)になったら学習が完了したとみなします。
作成したプログラムを以下に示します。
なお実行にはnumpyが必要ですのでインストールされていない場合はpipなどでインストールをしておいて下さい。
import numpy as np
action_str = {0: 'グー', 1: 'チョキ', 2: 'パー'}
class Agent:
def __init__(self):
self.__q_table = np.random.uniform(low=-1, high=1, size=(3, 3)) # Q値(状態(3)*行動(3)の2次元配列)
def get_action(self, state, episode):
epsilon = 0.5 * (0.99 ** episode) # epsodeを進めるにつれて小さくなる(0.5→0.068)
if epsilon <= np.random.uniform(0, 1):
# もしepisodeより一様乱数のほうが大きければ
# q_tableの中で現在の状態で最大の価値となる行動を選ぶ
action = np.argmax(self.__q_table[state])
else:
# episodeの確率でランダムな行動を取る
action = np.random.choice([0, 1, 2]) # 0:グー、1:チョキ、2:パー
return action
def update_q_table(self, action, state, next_state, reward):
# Qテーブルの更新
alpha = 0.2 # 学習率
gamma = 0.99 # 報酬の割引率
# 次に取る行動の候補(現在の状態でQ値を最大とする行動)
# 実際に次に取る行動ではなく、Qテーブルを更新するために使う
next_action = np.argmax(self.__q_table[next_state])
self.__q_table[state, action] = (1 - alpha) * self.__q_table[state, action] + \
alpha * (reward + gamma * self.__q_table[next_state, next_action])
def dump_q_table(self):
print('|状態(前回の相手の手)|行動(今回の自分の手)|Q値|')
print('|----|----|----|')
for state in range(3):
for action in range(3):
print(f'|{action_str[state]}|{action_str[action]}|{self.__q_table[state, action]}|')
class Environment:
def __init__(self):
self.state = np.random.choice([0, 1, 2]) # 状態(相手の出す手) 0:グー、1:チョキ、2:パー
self.__reward = { # 行動、状態に対する報酬
(0, 0): 0, (0, 1): 1, (0, 2): -1,
(1, 0): -1, (1, 1): 0, (1, 2): 1,
(2, 0): 1, (2, 1): -1, (2, 2): 0
}
def do_janken(self, action): # action: 行動(自分の出す手)
self.state = (self.state + 1) % 3 # 相手の手は、グー、チョキ、パーを順に繰り返す
reward = self.__reward[action, self.state]
return self.state, reward # 現在の状態と報酬
def reset(self): # 状態をリセットする
self.state = np.random.choice([0, 1, 2])
num_episodes = 5000 # 最大ゲーム数
max_number_of_steps = 100 # 1ゲーム内の最大ジャンケン数
agent_win_rate_list = [] # 各ゲーム内のエージェントの勝率を格納する配列
agent = Agent() # エージェント
env = Environment() # 環境
agent.dump_q_table()
for episode in range(num_episodes):
# ゲーム内で先に10勝した方が勝ち
# 環境の初期化
env.reset()
agent_win = 0
env_win = 0
for t in range(max_number_of_steps):
state = env.state
# 行動を決定
action = agent.get_action(state, episode)
# 行動を実行
# result_state: 行動の結果の環境の状態(相手の出した手)
# reward: 行動の結果得られた報酬
result_state, reward = env.do_janken(action)
# print(f'[{t}] {action_str[action]} x {action_str[result_state]}: {reward}')
if reward == 1:
agent_win += 1
elif reward == -1:
env_win += 1
# Q値を更新
agent.update_q_table(action, state, result_state, reward)
# agent.dump_q_table()
if agent_win == 10 or env_win == 10 or t == max_number_of_steps - 1:
# どちらかが10勝するかゲームの最大ジャンケン数に達したら終了
agent_win_rate = agent_win / (t + 1) # ゲーム内でのエージェントの勝率
agent_win_rate_list.append(agent_win_rate)
if agent_win == 10:
result = 'WIN'
elif env_win == 10:
result = 'LOSE'
else:
result = 'EVEN'
# print(f'episode {episode} finished. [{result}] / win rate {agent_win_rate}')
break
if (len(agent_win_rate_list) >=500 and np.sum(agent_win_rate_list[-500:]) >= 500):
# 500ゲーム連続で勝率10割だったら終了(学習の完了条件)
print(f'Episode {episode} train agent successfully!')
agent.dump_q_table()
break
# ジャンケン数の推移を描画
import matplotlib.pyplot as plt
plt.plot(agent_win_rate_list)
plt.xlabel('ゲーム')
plt.ylabel('ゲーム内での勝率')
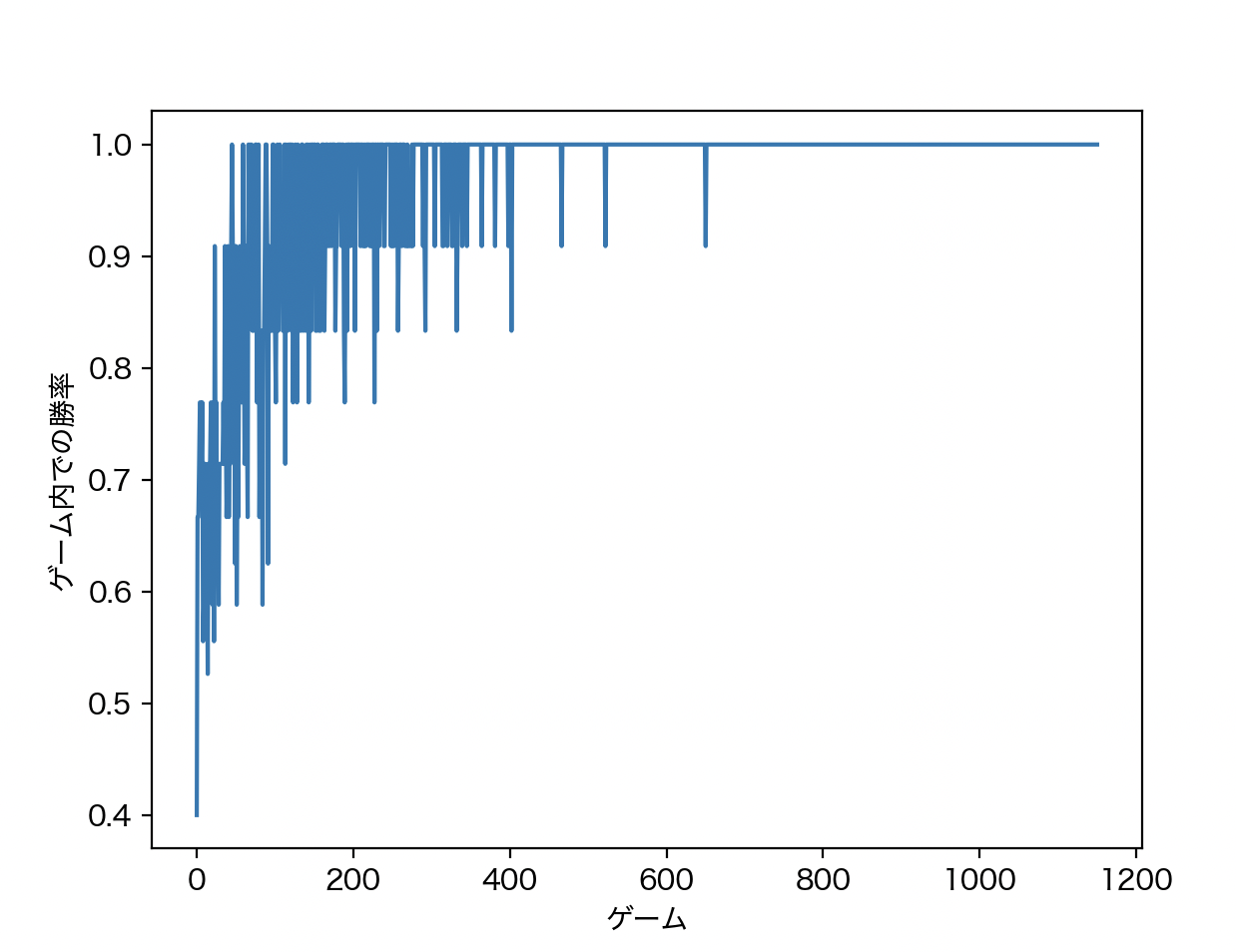
plt.show()下図は、学習の様子を表すグラフです。横軸は繰り返したゲーム数、縦軸は1ゲーム内でのエージェントの勝率です。
はじめのうちは、勝率が上がったり下がったりしながらも、全体的には上昇し学習が進んでいっていることが読み取れます。
そして、最終的には常に勝率10割となって学習が完了していることがわかります。
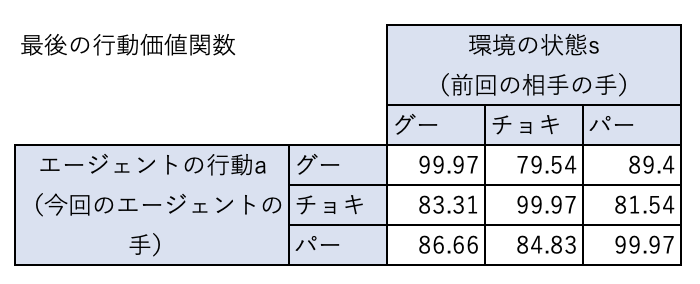
そして、下表は最終的なQテーブルの内容です。
エージェントが勝つ組み合わせ > あいこになる組み合わせ > エージェントが負ける組み合わせとなっていて、エージェントは最適な行動価値関数を学習できていることがわかります。
エージェントは何を学習しているのか?
ここで、エージェントが何を学習しているのかを考えてみましょう。
エージェントが知っているのは、自分も相手もグー、チョキ、パーのいずれを出すと勝敗が決まることだけです。
勝敗がどうやって決まるのかを知らないため、勝敗のルールを学ぶでしょう。
また、勝つために相手の癖を読むことも必要です。
こういったことが学習され、方策に反映されると考えられます。
次回は行動価値関数とその更新則の導出を、できるだけわかりやすく説明することを試みます。