本記事は、社内で行った「かな漢字変換と投機的デコーディング」の勉強会での資料を再構成したものです。
azooKey と Zenzai とは
azooKey は、Miwa氏(@miwa_ensan)によって、もともと iOS 用の IME として開発されてきた。
そこに電電猫猫/Naoki氏(@nya3_neko2)が参加して、これを macOS 上に移植し、さらにニューラル言語モデルを用いたかな漢字変換エンジン Zenzai の開発が始められたのが 2024年であり、これは IPA の未踏プロジェクトとして採択されている。
https://zenn.dev/azookey/articles/7a2c2d20a3cc4a
https://www.anlp.jp/proceedings/annual_meeting/2025/pdf_dir/P1-19.pdf
変換例:
https://x.com/miwa_ensan/status/1818545939134791903/video/1
https://x.com/nya3_neko2/status/1932739726009925796
超ざっくり説明
azooKey は形態素解析とNgramを基礎とする古典的な(それゆえに高速な)かな漢字変換システムだが、たいていの場合はこれだけでも十分な精度を持っている。
投機的デコーディングとは、メインのかな漢字変換処理を高速な azooKey に任せ、その変換結果の検証処理をニューラル言語モデルにやらせようというものである。検証結果で別候補が示されたら、それを採用した別解をazooKeyで再出力する。
azooKeyによってすでに文全体が変換済みであるので、その検証だけならニューラル言語モデルが並列に実行できるというところがミソである。
GPT-2 (Transformer) の基礎
Zenzai は言語モデルとして GPT-2 を利用しているので、まずは、その基本的なところから始める。
GPT-2 は Transformer のうち、Decoder部分のみを用いた、「自己回帰型の言語モデル(autoregressive language model)」となっている。
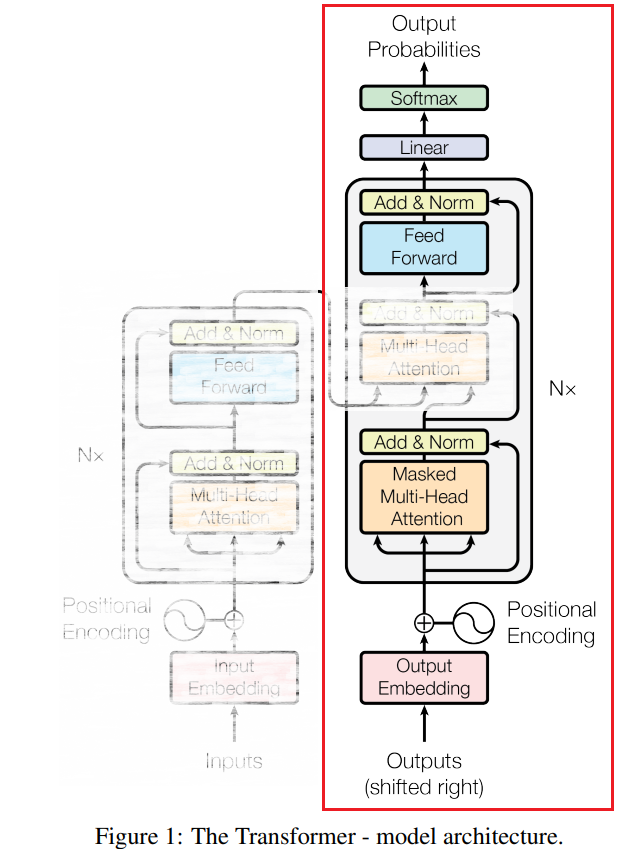
(Attention Is All You Need (https://arxiv.org/pdf/1706.03762) より引用、加工)
Encoderからの出力とのクロスアテンションの計算は行わない。
ここでは、入力データ自身が教師データになり、途中まで入力された文に対して、次の単語や文字(トークン)を予測(推論)することを学習する。たとえば、"I love cats very" という入力に対して、次の単語として "much" を出力するように学習する。
デコーダの処理の流れ
デコーダは本来、学習データを並列で処理するのだが、ここでは、理解しやすくするために、まず逐次処理として学習の流れを説明する。
学習データが "I love cats very much" だとする。
これを I, love, cats, very, much の5つの単語(トークン)に分割し、先頭から1つずつトークン数を伸ばしたトークン列を入力する。
上の例では、
I
I, love
I, love, cats
I, love, cats, very
I, love, cats, very, match
という5つのトークン列がデコーダに投入されることになる。
各トークン列に対して、以下のような処理が実行される。
[確率化 (Softmax)] (全トークンを底とした確率分布)
↑
[全トークン集合への射影演算 (Linear)] ←ここで最大のスコアが与えられたトークンが、予測された「次のトークン」となる
↑
[FFN (Feed Forward Networ; 2層パーセプトロン)]
↑
[残差と正則化 (Add & Norm]
↑
[自己注意の計算 (Masked Multi-Head Attention] (トークン間の関連度を示すマトリックスを出力)
↑
[位置情報の埋め込み (Positional Encoding] (トークン単位)
↑
[入力トークン列を埋め込みベクトル化 (Output Embedding)] (トークン単位)ここでのデコーダの出力は、全トークン集合を底とする確率分布になる(softmax)。
これと、正解トークンを表す確率分布、すなわち、入力トークン列の「次のトークン」(これが正解トークン)の確率が1で残りのトークンの確率が0であるような確率分布との間で、クロスエントロピーによる誤差計算を行う。
その結果を全入力トークン列で集計して1つの損失としてまとめ、それを使って誤差逆伝播でパラメータ更新を行う。
たとえば、 I, love, cats, very というトークン列に対して "much" の確率が 0.5, "well" の確率が 0.2, ... というような確率分布が出力されたとすると、これと正解トークンの確率分布 (much=1.0, well=0.0, ...) との間でクロスエントロピーの計算を行うということになる。
クロスエントロピーは、各トークンごとの確率(正確には尤度)の差分からなる一種の「距離」だと思ってよい
この一連の処理のうち、重要なのは「自己注意の計算」(Self Attention) と「全トークン集合への射影演算」(Linear)である。
自己注意計算では、入力トークン列の各トークン同士の一種の関連度合がスコア化される。縦横にトークンを並べ、その交点にスコアを記した表形式を思い浮かべるとよい。これをアテンションマトリクスと呼ぶこともある。
このアテンションマトリクスをいろいろいじった後に全トークン集合への射影演算が行われ、全トークンに対してスコアが付与される。「全トークン集合」とは文字通り、言語モデルが扱う全ての可能なトークンを集めたものである。そして全トークンの中から最大スコアを付与されたものが「次のトークン」として出力されることになる。
かな漢字変換用の学習
上の説明では、1つずつ長くなっていくトークン列が逐次的にデコーダに投入されるとしていたが、これ以降は、本来のデコーダの学習処理、すなわち、文全体からなるトークン列だけを投入して、デコーダ内部で上記処理(1つずつ長さを伸ばしたトークン列に対する処理)を並列で実行していくものとして説明する。
トークン
入力文や出力文をある単位で分割したもの。かな漢字変換の場合は、文字単位のトークンが使われる。
トークンは、最大でも 5千~6千個くらいに収める。それに当てはまらない文字はByte単位に分解される。
学習データ
以降は、次の例で説明していく。
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望してます<eoo>かな漢字変換においては、基本的に1文字が1トークンになるが、上の <boi>, <boo>, <eoo> は特殊なトークンであり、次のような意味を持つ。
<boi>: beginning of input<boo>: beginning of output<eoo>: end of output
<boi> から <boo> までが変換前の文字列、<boo>の次から <eoo> までが変換後の文字列である。
学習
学習は <boo> トークンから開始される。それ以前の「<boi>おんしゃをだいいちにしぼうしてます」に対しては学習を行わない(ここまではユーザーによる入力なので、学習をする必要がない)。
デコーダには、<boi>から<eoo>までの全文のトークンが投入されるが、内部で入力トークン列に対してマスクをかけて、長さが1ずつ増加するトークン列を生成する。そして学習処理の高速化のために、それらを並列で処理する。仮にGPUが搭載されておらず、CPUしか使えないPCであっても、マルチコアなCPUであれば、4並列や8並列といった並列化が可能である。
マスク
デコーダへの入力としては全文に対するトークンが与えられている。自己注意の計算は、先頭からある位置までのトークンを使って、次の位置のトークンを予測するためのものなので、次のトークン以降の「未来データ」を先読みしないようにするために、マスクが必要となると考えてもよい。
学習時の推論は、
<boo>以降の各入力トークンごとに行われるので、マスクの形状は以下ようになるだろう。0のところはトークンが存在しないものとして扱われる。<boi>, .., <boo>, ... <eoo>-1 [[1, 1, ..., 1, 0, 0, 0, ..., 0] [1, 1, ..., 1, 1, 0, 0, ..., 0] [1, 1, ..., 1, 1, 1, 0, ..., 0] ... [1, 1, ..., 1, 1, 1 ,1, ..., 1]]たとえば、
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望してます<eoo>という学習データに対して、上記のマスクを適用すると、
<boi>おんしゃをだいいちにしぼうしてます<boo>, 0,0,0,0, ..., 0 <boi>おんしゃをだいいちにしぼうしてます<boo>御, 0,0,0, ..., 0 <boi>おんしゃをだいいちにしぼうしてます<boo>御社, 0,0, ..., 0 <boi>おんしゃをだいいちにしぼうしてます<boo>御社を, 0, ..., 0 ... <boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望してま, 0 <boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望してますというトークン列が生成され、これらのトークン列に対する「次のトークン」の予測が、並列で学習処理される。
かな漢字変換の仕組み
辞書
ひらがな文字列をキーとして、その品詞や漢字形を与える辞書。
例
- おんしゃ: 御社,名詞
- おんしゃ: 恩赦,名詞
- を: を,格助詞
- しぼう: 志望,名詞:サ変
- しぼう: 死亡,名詞:サ変
- し: し,動詞,する,連用形
- て: て,接続助詞
- ます: ます,助動詞
Trie
トライ木(Trie)は、文字列の集合を効率よく表現・検索するための木構造の一種。
辞書のインデックスを構築する際によく用いられるデータ構造の一つ。
基本的な特徴
- 各ノードは1文字を表す。
- ルート(根)から葉に至るパスが文字列に対応する。
- 共通のプレフィックスを1つの経路として共有できる。
例
「cat」「car」「dog」を格納する Trie
(root)
├── c
│ └── a
│ ├── t (単語: cat)
│ └── r (単語: car)
└── d
└── o
└── g (単語: dog)
よく使われる trie
形態素解析器には、Patricia trie や Double array などがよく使われる。
- Patricia trie では、上の例でいうと、"ca" を1ノードにして、経路圧縮を図っている
- Double Array は、trie 構造を配列にマッピングすることで、超高速な検索を実現している
形態素解析
形態素解析器における Lattice(ラティス) は、入力された文のあらゆる形態素分割の可能性を表現する グラフ構造(有向グラフ) である。
ラティス
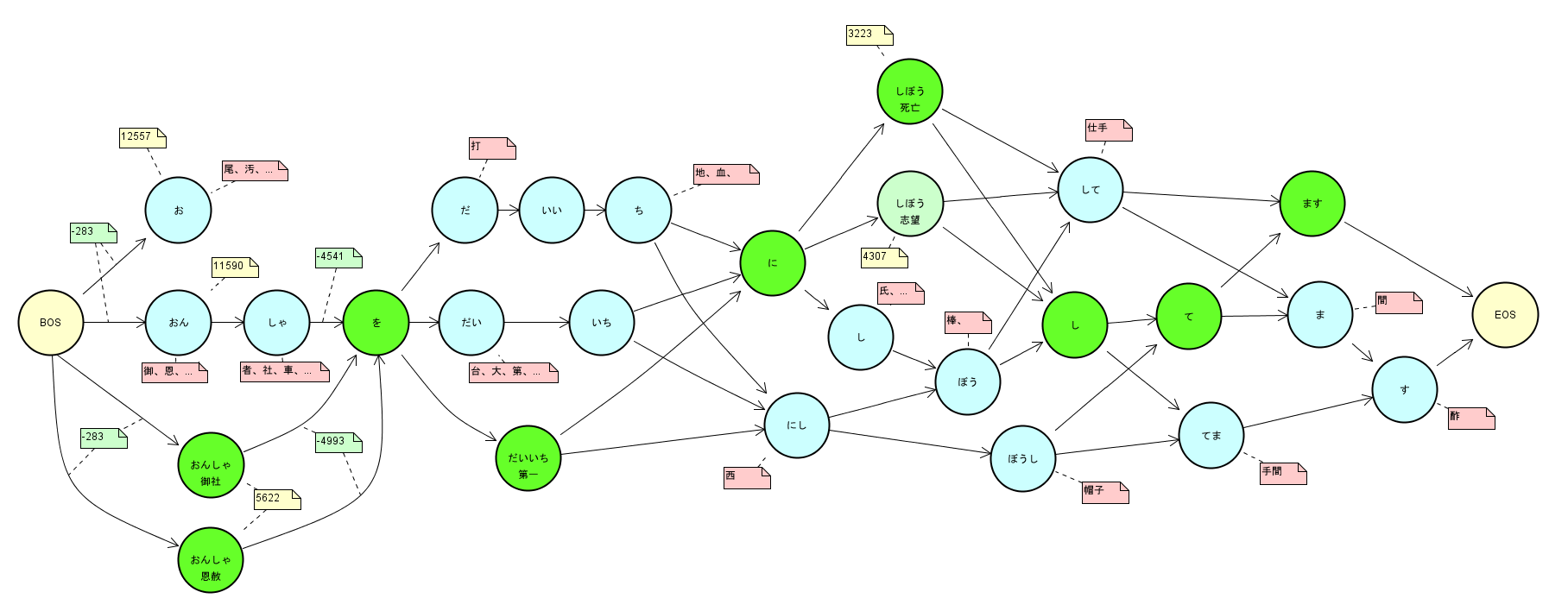
各ノードには形態素自身のコストが、またノード間には隣接する形態素間の接続コストが付与されている。
ここで、出現コストと接続コストの総和が最小になるようなパスを求めることが形態素解析の問題となる。
(上の図では、緑色のパスをたどると、総コストが最小になる。)
動的計画法
ラティス内の最小コストパスの選択問題として説明する。
「に」に至るあるパスのコストを考えてみる。たとえば、
PathCost([<BOS>, おん, しゃ, を, だ, いい, ち, に])は
PathCost([<BOS>, おん, しゃ, を, だ, いい, ち]) + ConnectionCost(ち, に) + NodeCost(に)で計算できる。ここで
ConnectionCost(ち, に) + NodeCost(に)は <BOS> から「ち」に至るどのパスのコストとも無関係に一意に定まる。したがって、<BOS> から「ち」を経由して「に」に至るパスの最小コストは
MinPathCost(<BOS>, ち, に) = MinPathCost(<BOS>, ち) + ConnectionCost(ち, に) + NodeCost(に) // 式 (A)となることがわかる。このことから、BOS から「に」に至る最小コストは、
MinPathCost(<BOS>, に)
= min(
MinPathCost(<BOS>, ち, に),
MinPathCost(<BOS>, いち, に),
MinPathCost(<BOS>, だいいち, に))
= min(
MinPathCost(<BOS>, ち) + ConnCost(ち, に) + Cost(に),
MinPathCost(<BOS>, いち) + ConnCost(いち, に) + Cost(に),
MinPathCost(<BOS>, だいいち) + ConnCost(だいいち, に) + Cost(に))で求められる。これを前方に繰り返していけば最終的に <BOS> にたどりつき、後方に伸ばしていけば最終的に <EOS> にたどりつく。
このように、全体的な最適化問題を部分の最適化問題に帰着できる場合に適用できる手法が動的計画法である。
辞書引きされた形態素からなるラティスにおけるパスのコスト計算は、まさにこの性質を持っているわけである。
なお、動的計画法の数学的な定式化については、金谷健一著『これなら分かる最適化数学』の第8章「動的計画法」が詳しい。
Viterbi アルゴリズム
形態素解析の話では、よく「Viterbi(ビタビ)」という言葉が出てくる。
Viterbiアルゴリズムは、動的計画法の一種であり、確率的な状態遷移モデル(特に隠れマルコフモデル:HMM)において、観測されたデータ列に対して最も尤もらしい隠れ状態列(パス)を効率的に求めるアルゴリズムである。
Viterbiアルゴリズムが扱うのは、以下のような問題である:
- 観測列: \( 𝑂 = (𝑜_1, 𝑜_2, ..., 𝑜_𝑇) \)
- 隠れ状態列: \(𝑆 = (𝑠_1, 𝑠_2, ..., 𝑠_𝑇)\)
- HMMの構成:
- 状態遷移確率: \(𝐴 = 𝑎_{𝑖𝑗} = 𝑃(𝑠𝑡 = 𝑗 ∣ 𝑠{t-1} = 𝑖) \) (ここにマルコフ性が効いている)
- 出力確率(尤度): \(𝐵 = 𝑏_𝑗(𝑜_𝑡) = 𝑃(𝑜_𝑡 ∣ 𝑠_𝑡 = 𝑗)\)
- 初期状態確率: \(𝜋_𝑖 = 𝑃(𝑠_1 = 𝑖)\)
形態素解析の場合では、
- 観測列: 入力文字列 (例: 御社を第一に志望してます)
- 隠れ状態列: 辞書引きされた形態素の品詞列 (例: 名詞, 格助詞, 名詞, 格助詞, サ変, 動詞, ...)
- 状態遷移確率: \(s_{t-1}\) の品詞と \(s_t\) の品詞との接続確率
- 出力確率: \(s_t\) の品詞 \(j\) から形態素 \(o_t\) が出現する確率 (例: サ変のうち、「志望」が出現する確率)
- 初期状態確率: \(𝜋_{BOS} = 𝑃(𝑠_1 = BOS) = 1\)
となるので、 Viterbi アルゴリズムを適用できるということになる。Viterbi では確率の積になっているが、対数を取ればその和として表されるので、本質的には上で説明した動的計画法のやり方と同じになる。
投機的デコーディングによる、言語モデルの実時間応用
投機的デコーディングとは
投機的デコーディング(Speculative Decoding)とは、小規模な言語モデルと大規模な言語モデルを組み合わせて、大規模モデルによる生成と同品質の出力を高速化するためのテクニックである。
簡単に言えば、「小さくて速いモデルで下書き(ドラフト)を出し、大きなモデルがそれを確認・修正する」という手法である。大きなモデルによる確認・修正は、学習時と同じ処理になるので並列に実行することが可能となる。大規模モデルのみで逐次的に生成を行うよりも、生成速度を向上させながら、出力品質を保つことができる。
ドラフトモデルの出力は、高速ではあるが誤りもしばしば含んでいる。つまり推論(デコード)時に、「まだ確実ではない出力を仮定して先に進めてしまう」という投機的(speculative)な動作に基づいているという点が「投機的」と名づけられた由縁であると思われる。
ドラフトモデルとターゲットモデル
- ドラフトモデル(小) 速くて軽いが、精度はほどほど
- ターゲットモデル(大) 精度は高いが、計算コストが大きい
手順
- ドラフトモデルでKトークン分を生成(例:4語分)
- ターゲットモデルで、それらKトークンが正しいかどうかを並列に評価
- 条件を満たせばそのまま採用、満たさなければ一部を修正
azooKey + Zenzai での投機的デコーディング
azookey + Zenzai では、
- azooKey (かな漢字変換器) がドラフトモデル
- GPT-2による言語モデルがターゲットモデル
になっている。
Zenzai のターゲットモデルは検証用として用いる
ドラフトモデルによる出力のうち、最良のものを選択するためにターゲットモデルを利用する。
ターゲットモデルの並列実行が高速化のカギ
学習時と同じことをやっている。
具体例
「おんしゃをだいいちにしぼうしてます」をドラフトモデル(azooKey)でかな漢字変換して「恩赦を第一に死亡してます」が得られたとする。
ターゲットモデルは「おんしゃをだいいちにしぼうしてます」に対して「御社を第一に志望してます」を出力するように学習されているとする。
ターゲットモデルは内部的に8並列で実行できるとすると、「<boi>おんしゃをだいいちにしぼうしてます<boo>恩赦を第一に死亡してます」をターゲットモデルに入力し、マスクを適切に設定することで、以下の8通りのトークン列に対して並列に(同時に)次の文字を出力させることができる。
<boi>おんしゃをだいいちにしぼうしてます<boo>
<boi>おんしゃをだいいちにしぼうしてます<boo>恩
<boi>おんしゃをだいいちにしぼうしてます<boo>恩赦
<boi>おんしゃをだいいちにしぼうしてます<boo>恩赦を
<boi>おんしゃをだいいちにしぼうしてます<boo>恩赦を第
<boi>おんしゃをだいいちにしぼうしてます<boo>恩赦を第一
<boi>おんしゃをだいいちにしぼうしてます<boo>恩赦を第一に
<boi>おんしゃをだいいちにしぼうしてます<boo>恩赦を第一に死ターゲットモデルは、1番目のトークン列に対して「御」を出力するが、これはドラフトモデルの「恩」とは異なる。そこで、ドラフトモデルに対して、「1文字目を『御』で始めよ」という制約を与える。ドラフトモデルはその制約に従って「御」で始まる解を出力する。その解が「御社を第一に死亡してます」だったとすると、次は「<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に死亡してます」がターゲットモデルへの入力となり、「御」までは確定しているので以下のトークン列を並列実行することになる。
<boi>おんしゃをだいいちにしぼうしてます<boo>御
<boi>おんしゃをだいいちにしぼうしてます<boo>御社
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に死
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に死亡6番目のトークン列からは「志」が出力されるが、これはドラフトモデルによる「死」とは異なるので、上と同じように「第一にの後は『志』で始めよ」という制約を返す。
ドラフトモデルは、再びこの制約に基づいて「御社を第一に志望してます」という解を出力してくる。
「御社を第一に志」までは正しいことが分かっているので、ターゲットモデルは以下のトークン列を並列実行することになる。
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望し
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望して
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望してま
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望してますこれで全てOKとなり、「御社を第一に志望してます」が変換結果として確定する。
もし、この変換をターゲットモデルだけでやらせるとすると、以下の処理を逐次的に実行する必要がある。
<boi>おんしゃをだいいちにしぼうしてます<boo> ⇒ 御
<boi>おんしゃをだいいちにしぼうしてます<boo>御 ⇒ 社
<boi>おんしゃをだいいちにしぼうしてます<boo>御社 ⇒ を
...
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望してま ⇒ す
<boi>おんしゃをだいいちにしぼうしてます<boo>御社を第一に志望してます ⇒ `<eoo>`誤解を恐れずに言えば、投機的デコーディングでは、ドラフトモデルの出力により「未来の文字」が分かっているのでターゲットモデルを並列で実行することが可能となって処理回数が3回で済んだが、ターゲットモデルだけで変換しようとすると、未来にどんな文字が出現するか分からないので逐次処理による12回の実行が必要になるということである。
ドラフトモデルによる高速な出力と、ターゲットモデルによる並列の検証。これが投機的デコーディングの速さの仕組みというわけである。

