ITの分野では「グラフ構造」というのが良く登場します。グラフ構造とは、簡単にいうと「モノとモノとの関係を図式的に表わしたもの」と言うことができます。下の図では、「Aさん」が「Bさん」のことを「好き!」という関係を表しています。

ただしこのグラフだけでは、BさんもAさんのことが好きかどうかは分かりません。この例のように、関係に向きがあるグラフを「有向グラフ」と呼んだりします。また上図の丸のことを「ノード」や「頂点」(vertex)、矢印のことを「辺」や「エッジ」と呼びます。
「GraphBLAS」は、基本的にはこのような有向グラフを線形代数の行列(Matrix)によって数学的に表現し、各種のグラフ演算を行列の演算に還元するためのツールです。
GraphBLAS 詳細についてはこちらの公式サイトや Wikipedia を見ていただくこととして、ここではその簡単な紹介をしたいと思います。
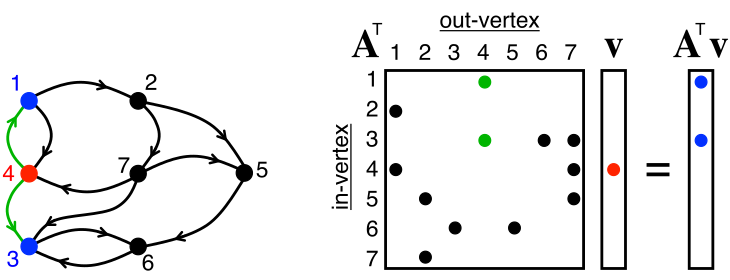
公式サイトには以下のような図が載っています。

同じ図が Wikipedia にも載っていて、そこには次のような説明が添えられています。(Googleによる翻訳)
- グラフの幅優先探索で 1 ステップを計算します。
- 行列ベクトル乗算を使用して、特定のソース頂点 (赤で表示) のアウトバウンド近傍 (青で表示された頂点 1 と 3) を計算できます。
- マトリックス \( A \) は、左側に示されているグラフの隣接行列であり、アウトバウンド エッジ (4,1) と (4,3) は緑色で示されています。
もう少しかみくだいて説明してみます。図の左側がグラフを図示したものです。青や赤や黒の丸がノードですね。右側の図がそれを行列(マトリックス)で表現したものです。(右図ではノードのことを vertex と表示している)
まず左図の赤い丸4に着目してみます。
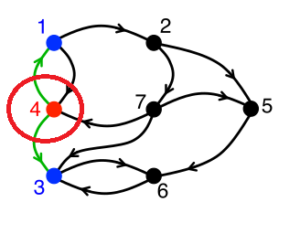
ノード4に向かう矢印を探すと、ノード1とノード7の2つあります。この状態を表しているのが、行列の行になります(下図)。
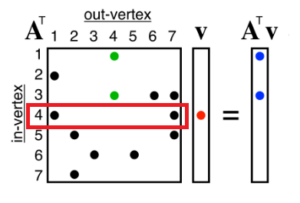
またノード4から出ていく矢印を探すと、ノード1とノード3があります。これが「アウトバウンド エッジ (4,1) と (4,3)」の意味です。この状態を表しているのが、行列の列になります(下図)。
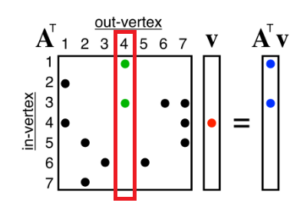
さてここでノード4から出ていく矢印の先にあるノードを表している列だけを取り出すにはどうしたらよいでしょうか。そのやり方を示しているのが、行列 \(A^{T}\) にかかっているベクトル \(V\) とその積の結果である \(A^{T}V\) です。
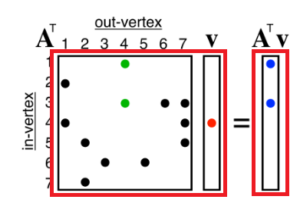
丸のところが 1 で、残りが 0 であるような行列、ベクトルをイメージしてください。その積を計算すると、 \( A^{T}V \) というベクトルが得られることが分かると思います。
上図の列ベクトル \(V\) は 行列 \(A^{T}\) から列4だけを取り出すものになっているわけですね。つまり、1回の行列演算で、あるノードからの行き先ノードを全て得ることができたわけです。これが「幅優先探索で 1 ステップを計算」ということの意味です。
このように、有向グラフの矢印を、その始点(列位置)と終点(行位置)で示される行列の位置に当てはめることで得られる行列のことを「隣接行列」と呼びます。
GraphBLAS はこの隣接行列を使った演算を高速に実行するライブラリを提供します。実際にこのライブラリを使ったGraphDBとして RedisGraph があります。当サイトの「最速のグラフデータベースRedisGraphをquickstartを30分でやってみた」でも紹介していますので、興味のある方は参照ください。